Chapter 3

Chapter 3 Self-Replication

The conception of a self-repairing and self-replicating FPGA presents a considerable challenge. If self-repair is a relatively well-investigated feature in the design of digital logic circuits, which implies the existence of a certain number of approaches to the implementation of self-repairing systems and thus an existing base for the development of our system, the same cannot be said for the property of self-replication: research in this domain is relatively scarce, particularly where hardware is concerned. This lack compelled us to develop an entirely new self-replication mechanism, allowing us to arrive at an efficient hardware realization.

We will begin this chapter with a short introduction to cellular automata, the computational model traditionally used in the study of self-replicating computing machines. We will then analyze existing self-replicating automata, and notably von Neumann's universal constructorand Langton's loop, before discussing the automata we developed in Embryonics. In the last section we will then describe the process we followed to adapt our self-replication mechanism to FPGAs.

3.1 Cellular Automata

The first phase of this development of our self-replicating system was, naturally, to examine the existing approaches in order to identify their strengths and weaknesses in relation to our requirements. Most, if not all, of the relevant research was applied to cellular automata (CA) [20, 60, 101, 109], a computational model which, while both ill-suited for hardware implementations and difficult to manipulate, nevertheless provides a relatively strict mathematical framework for the development of self-replicating machines, and has traditionally been the environment of choice for the study of such systems.

Cellular automata are arrays of elements, or cells¹², all behaving identically¹³, depending on the element's state. At regular, discrete intervals (iterations), the state of all elements is updated, depending on the current state of the element itself and that of its neighbors, according to a set of transition rules.

In order to illustrate the operation of cellular automata, we can examine one of the best known (and simplest) two-dimensional¹⁴ CA, commonly referred to as Life[32]. Life is a uniform two-dimensional cellular automaton where each element can be in one of only two states (aliveordead). The next state of an element depends on its current state and that of its eight closest neighbors (to the north, south, east, west, northeast, southeast, southwest, and northwest), and is calculated from a set of simple rules:

if fewer than two elements in the neighborhood are alive, the next state is dead (death by starvation);
if more than three elements in the neighborhood are alive, the next state is dead (death by overcrowding);
if exactly three elements in the neighborhood are alive, then the next state is alive (birth);
otherwise (i.e., if exactly two of the elements in the neighborhood are alive) the next state is equal to the current state (survival).

This very simple automaton is obviously not very powerful: the majority of initial configurations (the ensemble of the states of all elements at iteration 0) lead either to an empty space or to a collection of small, isolated cyclic patterns. One of the best-known of these patterns is the glider(Fig. 3-1, QT movie), a small structure capable of moving diagonally across the space. The glider is one of building blocks used to create machines which can become extremely complex (Fig. 3-2, QT movie).

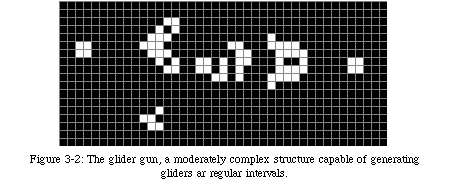
To resume, a cellular automaton is defined by the following parameters:

A number of dimensions, usually one or two, rarely three, and almost never four or more. All the automata used to model self-replication are two-dimensional, as is Life.
A set of states (two in the case of Life) and an initial configuration, defining the state of all the elements of the array at iteration 0. While there is no theoretical limit to the number of states in an automaton, for practical considerations very few automata use more than a handful.
A neighborhood, which specifies which neighbors will have an effect on an element's next state. By far the most common for two-dimensional automata are the neighborhood of 5 (the element itself plus its cardinal neighbors to the north, south, east, and west) and that of 9 (the element itself plus its neighbors to the north, south, east, west, northeast, southeast, southwest, and northwest). Life uses a neighborhood of 9.
A collection of transition rules, used to compute an element's next state depending on the neighborhood. The rules can be expressed either as an algorithm (as for Life above) or exhaustively as a lookup table¹⁵. In the latter case, the total number of rules necessarily to exhaustively define a cellular automaton is S^N, where S is the number of states and N the neighborhood (thus, to completely define Life, a lookup table of 2⁹=512 rules would be required). In practice, the number of required rules can, in many cases, be considerably reduced¹⁶, but the lookup table for a complex automaton (i.e., one with many states) can nevertheless reach a very important size.

As should now be obvious, cellular automata are not a model which can easily be applied to digital hardware. The need for each element to access the transition rules, coupled with the large number of elements required for complex behavior, is a serious drawback for an electronic implementation. In addition, while cellular automata can be a powerful model for certain kinds of applications where the transition rules are relatively simple and known in advance (e.g., the modelization of the behavior of gases), the design of a complex automaton is extremely difficult: the absence of global rules imply that complex automata (i.e., configurations which span a large number of elements) have to be handled exclusively at the local level, and no formal approach is available to aid in this task.

3.2 Von Neumann's Universal Constructor

The self-replication of digital logic circuits has thus far engendered a relatively modest amount of research, probably, as we mentioned, because of the technological problems associated with the implementation of such a feature. The existing approaches to the self-replication of computing systems are essentially derived from the work of John von Neumann [10], who pioneered this field of research. Unfortunately, the state of the art in the fifties restricted von Neumann's investigations to a purely theoretical level, and the work of his successors mirrored this constraint. In this section, we will analyze von Neumann's research on the subject of self-replicating computing machines, and in particular his universal constructor , a self-replicating cellular automaton [104].

3.2.1 Von Neumann's Self-Replicating Machines

Von Neumann, confronted with the lack of reliability of computing systems¹⁷, turned to nature to find inspiration in the design of fault-tolerant computing machines. Natural systems are among the most reliable complex systems known to man, and their reliability is a consequence not of any particular robustness of the individual cells (or organisms), but rather of their extreme redundancy. The basic natural mechanism which provides such reliability is self-reproduction¹⁸, both at the cellular level (where the survival of a single organism is concerned) and at the organism level (where the survival of the species is concerned).

Thus von Neumann, drawing inspiration from natural systems, attempted to develop an approach to the realization of self-replicating computing machines (which he called artificialautomata, as opposed to naturalautomata, that is, biological organisms). In order to achieve his goal, he imagined a series of five distinct models for self-reproduction [104, p. 91-99]: the kinematicmodel, the cellularmodel, the excitation-threshold-fatigue model, the continuousmodel, and the probabilisticmodel.

The kinematic model, introduced by von Neumann on the occasion of a series of five lectures given at the University of Illinois in December 1949, is the most general. It involves structural elements such as sensors, muscle-like components, joining and cutting tools, along with logic (switch) and memory elements. Concerning, as it does, physical as well as electronic components, its goal was to define the bases of self-replication, but was not designed to be implemented.
In order to find an approach to self-replication more amenable to a rigorous mathematical treatment, von Neumann, following the suggestion of the mathematician S. Ulam, developed a cellular model. This model, based on the use of cellular automata as a framework for study, was probably the closest to an actual realization. Even if it was never completed, it was further refined by von Neumann's successors and was the basis for all further research on self-replication.
The excitation-threshold-fatigue model was based on the cellular model, but each cell of the cellular automaton was replaced by a neuron-like element. Von Neumann never defined the details of the neuron, but through a careful analysis of his work, we can deduce that it would have borne a fairly close relationship to today's artificial neural networks, with the addition of some features which would have both increased the resemblance to biological neurons and introduced the possibility of self-replication.
For the continuous model, von Neumann planned to use differential equations to describe the process of self-reproduction. Again, we are not aware of the details of this model, but we can assume that von Neumann planned to define systems of differential equations to describe the excitation, threshold and fatigue properties of a neuron. At the implementation level, this would probably correspond to a transition from purely digital to analog circuits.
The probabilistic model is the least well-defined of all the models. We know that von Neumann intended to introduce a kind of automaton where the transitions between states were probabilistic rather than deterministic. Such an approach would allow the introduction of mechanisms such as mutation and thus of the phenomenon of evolution in artificial automata. Once again, we cannot be sure of how von Neumann would have realized such systems, but we can assume they would have exploited some of the same tools used today by genetic algorithms.

Of all these models, the only one von Neumann developed in some detail was the cellular model. Since it was the basis for the work of his successors, it deserves to be examined more closely.

3.2.2 Von Neumann's Cellular Model

In von Neumann's work, self-reproduction is always presented as a special case of universal construction, that is, the capability of building any machine given its description (Fig. 3-3). This approach was maintained in the design of his cellular automaton, which it therefore much more than a self-replicating machine. The complexity of its purpose is reflected in the complexity of its structure, based on three separate components:

A memory tape, containing the description of the machine to be built, in the form of a uni-dimensional string of elements. In the special case of self-reproduction, the memory contains a description of the universal constructor itself¹⁹ (Fig. 3-4).
The constructor itself, a very complex machine capable of reading the memory tape and interpreting its contents.
A constructing arm, directed by the constructor, used to build the offspring (i.e., the machine described in the memory tape). The arm moves across the space and sets the state of the elements of the offspring to the appropriate value.

The implementation as a cellular automaton is no less complex. Each element has 29 possible states, and thus, since the next state of an element depends on its current state and that of its four cardinal neighbors, 29⁵=20,511,149 transition rules are required to exhaustively define its behavior. If we consider that the size of von Neumann's constructor is of the order of 100,000 elements, we can easily understand why a hardware realization of such a machine is not really feasible.

In fact, as part of the Embryonics project, we did realize a hardware implementation of a set of elements of von Neumann's automaton [12, 89]. By carefully designing the hardware structure of each element, we were able to considerably reduce the amount of memory required to host the transition rules. Nevertheless, our system remains a demonstration unit, as it consists of a few elements only, barely enough to illustrate the behavior of a tiny subset of the entire machine.

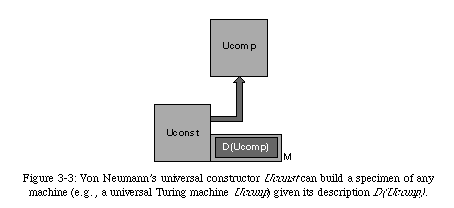
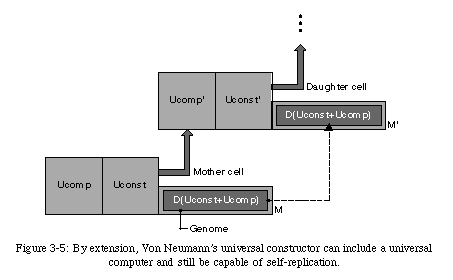
Before we continue, we should mention that von Neumann went one step further in the design of his universal constructor. If we consider the universal constructor from a biological viewpoint, we can associate the memory tape with the genome, and thus the entire constructor with a single cell (which would imply a parallel between the automaton's elements and molecules).

However, the constructor, as we have described it so far, has no functionality outside of self-reproduction. Von Neumann recognized that a self-replicating machine would require some sort of functionality to be interesting from an engineering point of view, and postulated the presence of a universal computer(in practice, a universal Turing machine, an automaton capable of performing any computation) alongside the universal constructor (Fig. 3-5).

Von Neumann's constructor can thus be regarded as a unicellular organism, containing a genome stored in the form of a memory tape, read and interpreted by the universal constructor (the mother cell) both to determine its operation and to direct the construction of a complete copy of itself (the daughter cell).

3.2.3 Von Neumann's Successors

The extreme size of von Neumann's universal constructor has so far prevented any kind of physical implementation (apart from the small demonstration unit we mentioned). But further, even the simulation of a cellular automaton of such complexity was far beyond the capability of early computer systems. Today, such a simulation is starting to be conceivable. Umberto Pesavento, a young Italian high school student, developed a simulation of von Neumann's entire universal constructor [78]. The computing power available did not allow him to simulate either the entire self-replication process (the length of the memory tape needed to describe the automaton would have required too large an array) or the Turing machine necessary to implement the universal computer, but he was able to demonstrate the full functionality of the constructor. Considering the rapid advances in computing power of modern computer systems, we can assume that a complete simulation could be envisaged within a few years.

The impossibility of achieving a physical realization did not however deter some researchers from trying to continue and improve von Neumann's work [11, 54, 71]. Arthur Burks, for example, in addition to editing von Neumann's work on self-replication [17, 104], also made several corrections and advances in the implementation of the cellular model. Codd [20], by altering the states and the transition rules, managed to simplify the constructor by a considerable degree. However, without in any way lessening these contributions, we can say that no major theoretical advance in the research on self-reproducing automata occurred until C. Langton, in 1984, opened a second stage in this field of research.

3.3 Langton's Loop

Von Neumann's Universal Constructor was so complex because it tried to implement self-reproduction as a particular case of construction universality, i.e. the capability of constructing any other automaton, given its description. C. Langton approached the problem somewhat differently, by attempting to define the simplest cellular automaton capable exclusively of self-reproduction.

As a consequence of this approach, his automaton, commonly known as Langton's Loop[53], is orders of magnitude simpler than von Neumann's. In fact, it is loosely based on one of the simplest organs²⁰ in Codd's automaton: the periodic emitter (itself derived from von Neumann's periodic pulser), a relatively simple structure capable of generating a repeating string of a given sequence of pulses.

Langton's loop (Fig. 3-6, QT movie) is named after the dynamic storage of data inside a square sheath (red in the figure). The data is stored as a sequence of instructions for directing the constructing arm, coded in the form of a set of three states. The data turns counterclockwise in permanence within the sheath, creating a loop.

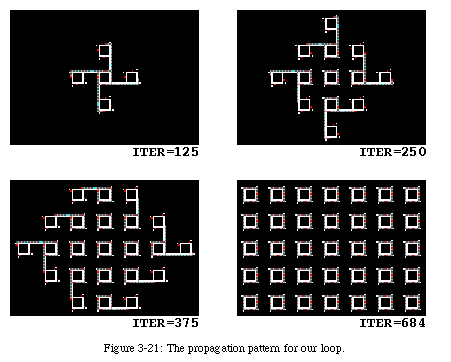
The two instructions in Langton's loop are extremely simple. One instruction (uniquely identified by the yellow element in the figure) tells the arm to advance by one position (Fig. 3-7), while the other (green in the figure) directs the arm to turn 90^o to the left (Fig. 3-8).

Obviously, after three such turns, the arm has looped back on itself (Fig. 3-9), at which stage a messenger (the pink element) starts the process of severing the connection between the parent and the offspring, thus concluding the replication process. Once the copy is over, the parent loop proceeds to construct a second copy of itself in a different direction (to the north in this example), while the offspring itself starts to reproduce (to the east in this example).

The sequential nature of the self-reproduction process generates a spiraling pattern in the propagation of the loop through space (Fig. 3-10, QT movie): as each loop tries to reproduce in the four cardinal directions, it finds the place already occupied either by its parent or by the offspring of another loop, in which case it dies (the data within the loop is destroyed).

Langton's loop uses 8 states for each of the 86 non-quiescent cells making up its initial configuration, a 5-cell neighborhood, and a few hundred transition rules (the exact number depends on whether default rules are used and whether symmetric rules are included in the count).

Further simplifications to Langton's automaton were introduced by Byl [18], who eliminated the internal sheath and reduced the number of states per cell, the number of transition rules, and the number of non-quiescent cells in the initial configuration. Reggia et al. [82] managed to remove also the external sheath, thus designing the smallest self-replicating loop known to date. Given their modest complexity, at least relative to von Neumann's automaton, all of the mentioned automata have been thoroughly simulated.

3.4 Self-Replicating Cellular Automata in Embryonics

While the self-replicating automata we introduced in this chapter are indeed interesting examples of self-replicating machines, they do not address some of the requirements of the Embryonics project. In this section, we will attempt to define more precisely these requirements and, after introducing a first attempt to augment the versatility of Langton's loop through the addition of a Turing machine, we will present a new self-replicating automaton we developed in order to offset some of the more important deficiencies. We will begin by describing in some detail the operation of the new loop in its most basic configuration, and then illustrate an example of a more elaborate version where a program has been added to the basic automaton to demonstrate its construction capabilities.

3.4.1 The Requirements of the Embryonics Project

Langton's loop represents the best-known example of a simple self-replicating machine, and is therefore of great interest for the Embryonics project. However, it falls short of our requirements in two important aspects:

It is designed to operate in an infinite space, whereas the surface of an integrated circuit is necessarily finite. This inconvenience, which might appear relatively minor and easily circumvented, is in fact a major obstacle: the loop's mechanism of self-replication (i.e. the arm) is inherently incapable of handling contact with the array's border.
It does not have any functionality beyond self-replication: the loop reproduces and then dies. It is thus more similar to a biological (or even a software) virus than to an actual cell. Once again, the default is structural: because of its origins in the periodic emitter, all the data circulating inside the loop is involved in the generation of the sequence which directs the self-replication process. As we will see, while it is possible to add functionality to Langton's loop, the task is extremely complex and the results not very efficient.

Nevertheless, von Neumann's constructor and Langton's loop are the models which most closely approach our requirements. Therefore, we decided to follow tradition in developing our own approach to self-replication by using cellular automata as an environment to study the issue.

As we already mentioned, there is no formal approach to the development of complex cellular automata. The design of such systems poses therefore considerable problems, since few of the available tools are suited for the task. In particular, no efficient tools were available to help the user in determining the local transition rules necessary to obtain a complex global behavior (cellular automata are mostly used to simulate physical phenomena, where the rules are usually well known). Our first task was therefore to design a software application which would allow us to generate the required rules as easily as possible. The resulting program (described in Appendix A) is, to the best of our knowledge, unique, and proved an invaluable tool in our research.

Equipped with a reasonably powerful tool, we started developing a new automaton capable of self-replication. Considering the complexity of von Neumann's constructor, we decided to draw inspiration from the much simpler Langton's loop, but, as we will see, we had to develop a completely novel mechanism to enable us to circumvent its drawbacks.

3.4.2 A Self-Replicating Turing Machine: Perrier's Loop

As we mentioned, one of the two main problems of Langton's loop is that it is not well adapted to finite CA arrays. Its self-reproduction mechanism assumes that there is enough space for a copy of the loop, and the entire loop becomes non-functional otherwise.

At first glance, this might seem a relatively trivial drawback, which could be overcome by modifying the loop. Such a modification, however, turns out to be very difficult. In fact, to exist in a finite space, and assuming that the automaton has no a prioriknowledge of the location of the boundaries (a safe assumption, since CA elements have only knowledge of their immediate neighborhood), the loop needs either to verify that enough space is available before it starts the replication process, or else some way to destroy the constructing arm if it detects a boundary during the self-replication process. Either of these mechanisms would require a major structural modification to Langton's loop.

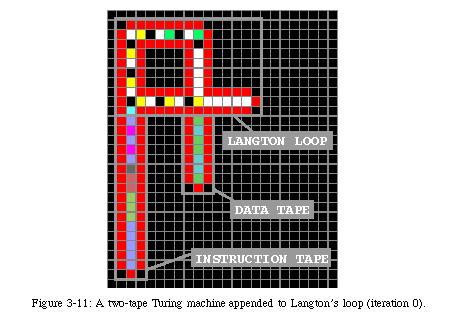
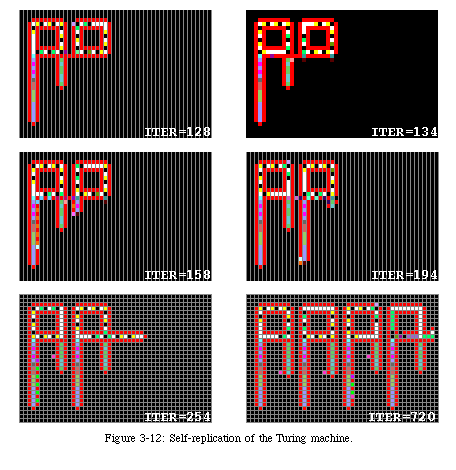
Thus, rather than trying to adapt Langton's automaton to a finite space, we decided to develop an entirely new mechanism, designed specifically to exist in a finite, but arbitrarily large, space, and at the same time capable, unlike Langton's loop, to have a functionality in addition to self-replication. Adding functionality to Langton's loop, in fact, is not possible without major alterations. As a matter of fact, in the course of our research, we did develop a relatively complex automaton (Fig. 3-11, QT movie) in which a two-tape Turing machine was appended to Langton's loop [77]. This automaton, developed in our laboratory by J.Y. Perrier as a semester-long research project under the supervision of Prof. J. Zahnd, exploits Langton's loop as a sort of "carrier" (Fig. 3-12, QT movie): the first operation of Perrier's loopis to allow Langton's loop to build a copy of itself (iteration 128: note that the copy is limited to one dimension, since the second dimension is taken up by the Turing machine). The main function of the offspring is to determine the location of the copy of the Turing machine (iteration 134). Once the new loop is ready, a "messenger" runs back to the parent loop and starts to duplicate the Turing machine (iterations 158 and 194), a process completely disjoint from the operation of the loop. When the copy is finished (iteration 254), the same messenger activates the Turing machine in the parent loop (the machine had to be inert during the replication process in order to obtain a perfect copy). The process is then repeated in each offspring until the space is filled (iteration 720: as the automaton exploits Langton's loop for replication, meeting the boundary of the array causes the last machine to crash).

The automaton thus becomes a self-replicating Turing machine, a powerful construct which is unfortunately handicapped by its complexity: in order to implement a Turing machine, the automaton requires a very considerable number of additional states (more than 60), as well as an important number of additional transition rules. This kind of complexity, while still relatively minor compared to von Neumann's universal constructor, is nevertheless too important to be really considered for a hardware application. So once again, adapting Langton's loop to fit our requirements proved too complex to be efficient, and we were forced to design a novel automaton to meet our requirements.

3.4.3 A Novel Self-Replicating Loop: Description

In designing our self-replicating automaton [97], we did maintain some of the more interesting features of Langton's loop. In particular, we preserved the structure based on a square loop to dynamically store information. Such storage is convenient in CA because of the locality of the rules. Also, we maintained the concept of constructing arm, in the tradition of von Neumann and his successors, even if we introduced considerable modifications to its structure and operation.

While preserving some of the more interesting features of Langton's loop, we nevertheless introduced some basic structural alterations:

We use a 9-element neighborhood (the element itself plus its 8 neighbors).
As in Byl's version of Langton's loop, we use only one sheath, but contrary to Byl, we retain the internal sheath and eliminate the external one. This allows us to let the data in the loop circulate without the need for leading or trailing states (the black and white elements in Langton's loop). In addition to the internal sheath, we have four gate elements (in the same state as the sheath) outside the loop at the four corners of the automaton. These elements are initially in the "open" position, and will shift to the "closed" position once the copy is accomplished.
We extend four constructing arms in the four cardinal directions at the same time, and thus create four copies of the original automaton in the four directions in parallel. When the arm meets an obstacle (either the boundary of the array or an existing copy of the loop), it simply retracts and puts the corresponding gate element in the closed position. This mechanism allows us to overcome the first major drawback of Langton's loop in relation to the Embryonics project (its inability to work properly in a finite space).
Rather than being directed to advance, our constructing arm advances by default. As a consequence, it is necessary only to direct it to turn at the appropriate moment. This is done by sending periodic "messengers" to the tip of the constructing arm.
The arm does not immediately construct the entire loop. Rather, it constructs a sheath of the same size as the original. Once the sheath is ready, the data circulating in the loop is duplicated and the copy is sent along the constructing arm to wrap around the new sheath. When the new loop is completed, the constructing arm retracts and closes the gate. As we will see, dividing the self-replication process in two phases is a major asset in the transition to digital hardware.
As a consequence, we use only four of the circulating elements to generate the messengers. Since the only operation performed on the remaining data elements is duplication, they do not have to be in any particular state. In particular, they can be used as a "program", i.e., a set of states with their own transition rules which will then be applied alongside the self-reproduction to execute some function, allowing us to overcome the second drawback of Langton's loop (its lack of functionality beyond self-reproduction).
Unlike Langton's loop, our loop does not "die" once duplication is achieved, as the circulating data remains untouched by the self-reproduction process. This feature is a requirement for implementing functions which work after the copy has finished. As a side benefit, it becomes possible to force the loop to try and duplicate again in any of the four directions simply by shifting the corresponding gate back to the open position. This feature could be interesting in view of self-repair: a dead loop can be reconstructed by its neighbors.

As should be obvious, while our loop owes to von Neumann the concept of constructing arm and to Langton (and/or Codd) the basic loop structure, it is in fact a very different automaton, endowed with some of the properties of both.

We have seen that von Neumann's automaton is extremely complex, while Langton's loop is very simple. The complexity of our automaton is more difficult to estimate, as it depends on the data circulating in the loop. The number of non-quiescent elements making up the initial configuration depends directly on the size of the circulating program. The more complex (i.e. the longer) the program, the larger the automaton (it should be noted, however, that the complexity of the self-reproduction process does not depend on the size of the loop). The number of states also depends on the complexity of the program. To the 5 "basic" states used for self-reproduction (see description below) must be added the "data states" (at least one) used in the program, which must be disjoint from the basic states. The number of transition rules is obviously a function of the number of data states: in the basic configuration (i.e., one data state), the automaton needs 692 rules²¹ (173 rules rotated in the four directions).

The complexity of the basic configuration is therefore in the same order as that of Langton's and Byl's loops, with the proviso that it is likely to increase drastically if the data in the loop is used to implement a complex function.

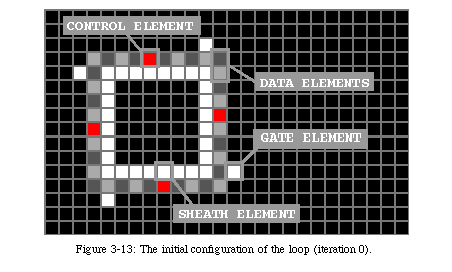
3.4.4 A Novel Self-Replicating Loop: Operation

As for von Neumann's and Langton's automata, the ideal space for our automaton is an infinite two-dimensional grid. Since we realize that a practical implementation of such a space might prove difficult, we added some transition rules to handle the collision between the constructing arm and the border of the array. On meeting the border, the arm will retract without attempting to make a copy of the parent loop.

The elements of the array require five basic states and at least one data state (Fig. 3-13, QT movie). State 0 (black) is the quiescent state: it represents the inactive background. State 1 (white) is the sheath state, that is the state of the elements making up the sheath and the four gates. State 2 (red) is the activation stateor control state. The four elements in the loop directing the reproduction are in state 2, as are the messengers which will be used to command the constructing arm and the tip of the constructing arm itself for the first phase of construction, after which the tip of the arm will pass to state 3 (light blue), the construction state. State 3 will construct the sheath that will host the offspring, signal the parent loop that the sheath is ready, and lead the duplicated data to the new loop. State 4 (green), the destruction state, will destroy the constructing arm once the copy is completed. In addition to these states, two additional data states(light and dark grey) represent the information stored in the loop. In this example, they are inactive, while the next section describes a loop where they are used to store an executable program.

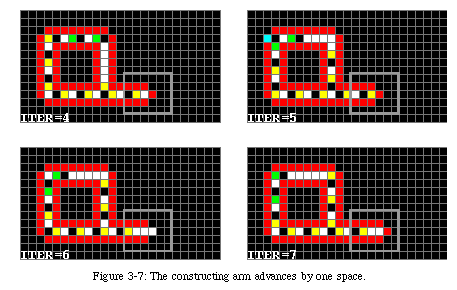
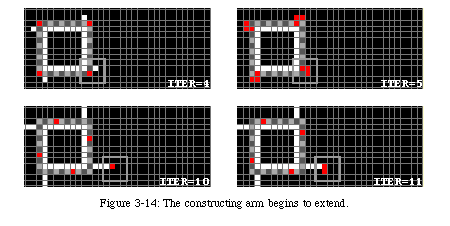
The initial configuration is in the form of a square loop wrapped around a sheath. The size of the loop is variable, and for our example is set to 8x8. In the loop is a string of elements of which four are in the activation state (red) and are placed at a distance from each other equal to the side of the loop. Near the four corners of the loop we have placed four elements in the sheath state. These are the gate elements, and the position they occupy at iteration 0 means that the gates are open (that is, that the automaton should attempt to duplicate itself in all four directions).

Once the iterations begin, the data starts turning counterclockwise around the loop. Nothing happens until the first control element reaches a corner of the loop, where it checks the status of the gate. Since the gate is open, the control element splits into two identical elements: the first continues turning around the loop, while the second starts extending the arm (Fig. 3-14). The arm advances by one position every two iterations.

Once the arm has started extending, each control element that arrives to a corner will again split and one of the copies will start running along the arm, advancing by one position per iteration (Fig. 3-15). Since the arm is extending at half the speed of the messengers and the messengers are spaced 8 elements apart (the length of one side of the loop), the messengers will reach the tip of the arm at regular intervals corresponding to the length of one side of the loop.

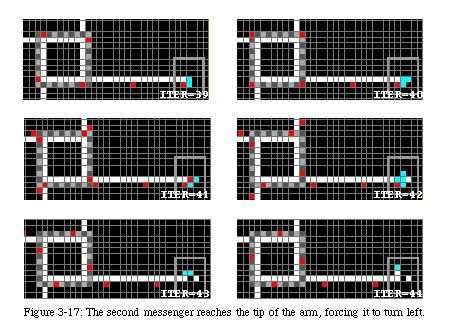
When the first messenger reaches the tip of the arm, the tip, which was until then in state 2, passes to state 3 and continues to advance at the same speed (Fig. 3-16). This transformation tells the arm that it has reached the location of the offspring loop and to start constructing the new sheath.

The next three messengers will force the tip of the arm to turn left (Fig. 3-17), while the fourth will reach the tip as the arm is closing upon itself (Fig. 3-18). It causes the sheath to close and then runs back along the arm to signal to the original loop that the new sheath is ready.

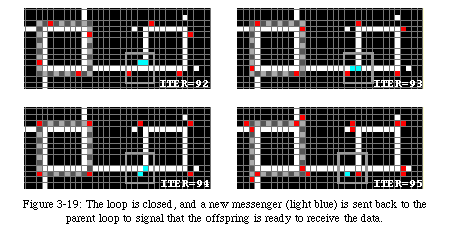
Once the return signal arrives at the corner of the original loop, it waits for the next control element to arrive (Fig. 3-19). When the control element sees the messenger waiting by the gate, once again it splits, one copy staying around the loop, the other running along the arm. This time, however, rather than running along the arm in isolation as a messenger, it carries behind him a copy of the data in the loop.

Always followed by the data, it runs around the sheath until it has reached the junction where the arm folded upon itself (Fig. 3-20). On reaching that spot, it closes the loop and sends a destruction signal (green) back along the arm. The signal will destroy the arm until it reaches the corner of the original loop, where it closes the gate to avoid further copies.

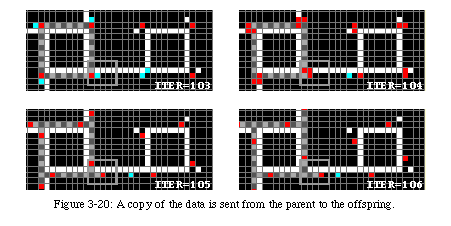
Meanwhile, the new loop is already staring to reproduce itself in three of the four directions. One direction (down in the figures) is not necessary since another of the new loops will always get there first, and therefore its corresponding gate is automatically set to the closed position. Since the automaton reproduces in all four directions at the same time, its propagation pattern (Fig. 3-21, QT movie) is somewhat different from that of Langton's loop.

After 121 time periods the gates of the original automaton will be closed and it will enter an inactive state, with the understanding that it will be ready to reproduce itself again should the gates be opened.

The main advantage of the new mechanism is that it becomes relatively simple to retract the arm if an obstacle (either the boundary of the array or another loop) is encountered, and therefore our loop is perfectly capable of operating in a finite space. In the example above, the right border of the figure corresponded to the boundary of the array: when the offspring tried to replicate towards the east, the arm, it found its way blocked, simply retracted and closed its gate (Fig. 3-22).

3.4.5 A Novel Self-Replicating Loop: a Functional Example

In Fig. 3-23 (QT movie) , we illustrate an example of how the data states can be used to carry out operations alongside self-reproduction. The operation in question is the construction of three letters, LSL (the acronym of Logic Systems Laboratory), in the empty space inside the loop. Obviously this is not a very useful operation from a computational point of view, but it is a far from trivial construction task which should suffice to demonstrate the capabilities of the automaton.

For this example, we have used 5 data states, each representing an instruction for the construction of the letters: advance, turn left, turn right, empty space, and a NOP (no operation) instruction to fill the remaining space in the loop. The construction requires 330 additional rules.

The operation of the program is fairly straightforward. When a certain initiation sequencewithin the loop arrives to the top left corner of the loop, a "door" is opened in the internal sheath (Fig. 3-24). The rest of the program, as it passes by the door in its rotation around the loop, is duplicated and one of the copies is sent to the interior of the loop, where it is treated as a sequence of instructions which direct the construction of the three letters. Once the duplication is complete (i.e., when the first NOP instruction reaches the opening), the door is closed and the sheath reset, except for a flag which indicates that the task has already been completed and prevents the door from being opened again (Fig. 3-25).

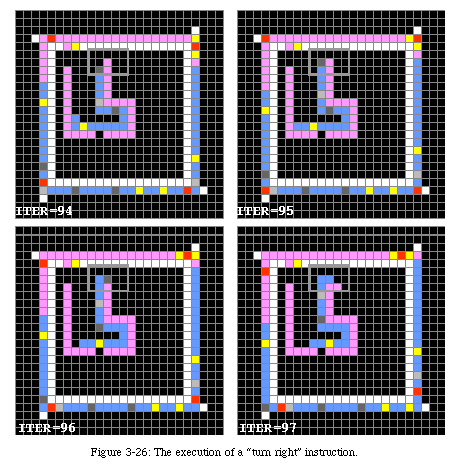
The construction mechanism itself is somewhat similar to the method Langton used in his own loop, and is based on a modified constructing arm. The advance instruction causes the arm to advance by one element, the turn left and turn right (Fig. 3-26) instructions cause the arm to change direction, and the "empty space" instruction produce a gap in the arm (to separate the letters).

During the process of reproduction, the program is simply copied (as opposed to interpreted as in the interior of the sheath) and arrives intact in the new loop, where it will execute again exactly as it did in the parent loop (Fig. 3-27, QT movie).

This is a simple demonstration of one way in which the data in the loop could be used as an executable program. Of course, many other methods can be envisaged, but unfortunately it would be very hard, if not impossible, to obtain computationally interesting self-replicating systems using "pure" cellular automata.

In fact, CA are, by definition, closed systems: all the information must be present in the array at iteration 0 (in our case, all the data for the system must be included in the initial loop). Since useful computation would require that each of the offspring execute a different function (or at the very least, the same function on different data), the requirement that all information be stored in the parent loop is too restrictive for our needs.

At this stage we therefore decided to stop further development of self-replicating machines in the cellular automaton environment, and attempt to transfer the accumulated experience to the design of our FPGA.

3.5 Towards a Digital Hardware Implementation

An FPGA circuit is significantly different from a cellular automaton, a certain superficial resemblance notwithstanding. To develop a self-replication mechanism which can be efficiently adapted to digital electronic circuits in general and to FPGAs in particular, we therefore had to analyze the operation of our loop and attempt to extract not so much the precise mechanism used to achieve self-replication, but rather the general approach to the problem. In this section, we will present the results of this process, which led to the development of the membrane builder, a very simple cellular automaton which we then implemented in hardware and integrated into our FPGA.

3.5.1 The Membrane Builder

Our automaton fits most of our requirements: it is a computing machine (it would be possible, if difficult, to add a universal Turing machine to the loop) capable of self-replication. The transition from cellular automata to hardware, however, requires a process of synthesis: CAs, as we have seen, are very inefficient from the point of view of an hardware realization (every element needs to access a substantial lookup table), hard to design (even with our dedicated tool, the design of a complex automaton remains a daunting endeavor), and fragile (a single faulty element almost invariably destroys the entire system). To find a viable approach to the realization of self-replicating hardware, we thus had to extract from our automaton the essential features of the self-replicating mechanism, and use them as a basis for the design of an electronic circuit.

One of the main differences between our loop and Langton's lies in the two-phase mechanism of self-replication: while in Langton's loop the process is indivisible, we can identify two distinct phases in the self-replication of our loop: first the arm "reserves" the space required for the offspring, and only then the data are copied. In other words, the process can be divided into a structural phase, where the structure of the loop is set into the empty space, and a configuration phase, where the functionality of the parent is sent into the offspring.

In defining an FPGA architecture to implement the process of self-replication, the requirements of cellular automata conflict with an efficient use of hardware in a number of respects, notably where the configuration phase is concerned: the loop structure, so well suited to cellular automata, represents an unacceptable waste of material in an electronic circuit (using the loop's perimeter implies that the interior is wasted). As we will see in the next chapter, to efficiently exploit the surface of programmable logic we adopted a more conventional approach to the configuration of the array. However, the separation between the two phases of our self-replication strategy means that the drawbacks of the configuration phase need not necessarily apply to the structural phase.

The greatest obstacle in implementing self-replication in our FPGA lies in the fact that we cannot a prioridefine the size of our cells. Thus, we require a system capable of configuring a finite two-dimensional array of elements (the FPGA) as a two-dimensional array of identical configuration blocks, each containing a single cell. Obviously, this problem bears a considerable resemblance to self-replication in cellular automata: similarities exist between the CA elements and the FPGA elements (molecules) and between a loop and a processor (cells). By exploiting this resemblance, we can observe that the structural phase of our self-replication mechanism can indeed be a solution to the problem of configuring our FPGA.

If we consider the FPGA before configuration as an array of CA elements in the quiescent state, we can design a very simple automaton [60, 92] (Fig. 3-28, QT movie) capable of subdividing the surface of programmable logic into square blocks of variable size (we thank André Stauffer for the realization of this automaton). The initial configuration (iteration 0) of this automaton is somewhat non-conventional: the configuration of an FPGA is effected by a one-dimensional sequence of bits (the configuration bitstream), while conventional cellular automata operate from an initial two-dimensional structure already in place at iteration 0. To overcome this difference, we designed an initial configuration which simulatesa configuration stream: the sequence of states stored alongside the (inert) white band represents the data stored in a memory, and as time progresses it slides along the band to enter the quiescent area (the empty FPGA) from its lower left corner.

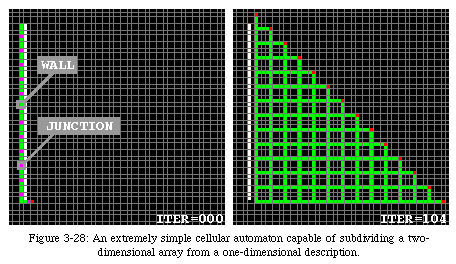
The mechanism used in this automaton is very similar to the one used to direct the constructing arm in our loop, but is much simpler. It uses only two active states²²: a wall state(green), which defines the borders of the blocks, and a junction state(purple), which defines the intersections between walls. Operation starts when the first data element (always in the junction state) leaves the inert band. From this first element, two branches start to propagate: one to the north and one to the east. The branches will advance at half speed, leaving walls on their path. Meanwhile, data is leaving the band at full speed. Whenever a junction state reaches the tip of the branches, it causes a further split: again, one branch to the north and one to the west. It should then be obvious that in the end, the quiescent area will have been divided into square blocks of a size corresponding to the distance between two junction states in the data tape.

This very simple cellular automaton could thus allow us to achieve self-replication in an FPGA by transforming a one-dimensional string of information to a two-dimensional array of square blocks of programmable size: the elements of the cellular automaton form the perimeter of the block, and thus perform the same function as the membranewhich surrounds a biological cell. Moreover, the automaton is simple enough that a hardware implementation becomes straightforward.

3.5.2 A Self-Replicating FPGA

The next step in implementing a self-replicating FPGA is to integrate the automaton into the two-dimensional array of programmable elements. After experimenting with different alternatives, we decided to insert the CA elements in the space between the FPGA elements (Fig. 3-29). The configuration stream enters the array in the southwest corner, and propagates through the automaton: this operation is completely independent of the structure of the programmable elements, and can thus be applied to any FPGA architecture.

Fig. 3-30 shows the effect of entering the simple state sequence shown in Fig. 3-29 into the automaton. As for the automaton described above, only two active states are used: the wall state, labeled 1, and the junction state, labeled 2. The operation of this automaton is identical to that of the one shown in the previous subsection, with a single exception: the corners of the blocks remain in a distinctive junction state after the end of the propagation. This small difference, which in fact allows us to reduce the complexity of the hardware, is a typical example of the difficulties of designing a cellular automaton for hardware implementation: an increase in the complexity of the automaton can, as often as not, result in a decrease in the complexity of the hardware required to implement it.

In the end, we were able to design an extremely simple mechanism which allows us to partition the FPGA into a set of square blocks of programmable size (shown in Fig. 3-31 with a more intuitive symbolic representation of the CA states), the indispensable preamble to self-replication. Once the membrane is in place, we can, as we will see in the next chapter, use it to direct the configuration of the FPGA: we can exploit the information contained in the cellular automaton to automatically replicate the configuration of a single block into all of the blocks in parallel. We can, in short, achieve the self-replication of electronic circuits²³ .

12.Again, standard terminology creates a problem with regards to our project. The elements of cellular automata are usually referred to as cells, but do not really resemble biological cells (they do not contain a genome). We will thus call them elements or sometimes molecules, the closest biological analog.

13.Elements with different behaviors are allowed in some CAs, usually called non-uniform. Since all the models used in this thesis are uniform, however, we can consider all elements to have identical behavior.

14.There is no theoretical limit to the number of dimensions of a cellular automaton. However, CA being, essentially, graphic-oriented models, the need to display their activity imposes a practical limit: the greatest majority of existing automata are either one- or two-dimensional, and while we are aware of the existence of some three-dimensional automata, we have no knowledge of any implementation in four or more dimensions. All of the automata used to study self-replication are two-dimensional.

15.A typical lookup table entry for a 2-state 9-neighbors automaton would have the form:

0,0,0,0,1,0,1,1,0=1; where the first nine values represent the current state of the neighborhood and the last is the next state.

16.For example by assuming a "default" behavior (e.g., the next state will remain equal to the current state unless a rule specifies otherwise).

17.Let us remember that the computers von Neumann was familiar with were based on vacuum-tube technology, and that vacuum tubes were much more prone to failure than modern transistors. Moreover, since the writing and the execution of complex programs on such systems represented many hours (if not many days) of work, the failure of a system had important consequences in wasted time and effort.

18.You will note that we use the terms self-replication and self-reproductioninterchangeably. In reality, the two terms are not really synonyms: self-reproduction is more properly applied to the reproduction of organisms, while self-replication concerns the cellular level. As we will see, the more correct term to use in this circumstance would probably be self-replication, but since von Neumann favored self-reproduction, we will ignore the distinction.

19.The memory of von Neumann's automaton bears a strong resemblance to the biological genome. This resemblance is even more remarkable when considering that the structure of the genome was not discovered until after the death of von Neumann.

20.An organ in this context can be seen as a self-supporting structure capable of a single sub-task.

21.By default, all elements remain in the same state.

22.Some additional states are indeed required for the operation of the automaton, but they are either inert (e.g., the black quiescent state and the white band) or transient.

23.The process also resembles the biological process of cloning. It is self-replication in the sense that it is handled by the hardware itself, and it is cloning in the sense that all data come from an external source.